Square Area....

*click to make bigger*

Definition:

 A Square is a flat shape with 4 equal sides and every angle is a right angle (90°) and opposite sides are parallel.

Diagonals...

A square has two diagonals, they are equal in length and intersect at the middle point.

The Diagonal is the side length(a) times the square root of 2:
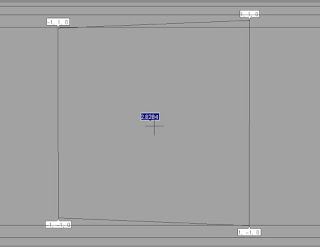
*side length = a = the length between A and D* (see image at top)

Diagonal "d" = a × √2

 

Perimeter...

The Perimeter is 4 times the side length:

Perimeter "p" = 4a

Area...

The Area is the side length squared:

Area = a² = a × a

....or half of the diagonal squared:

 

Area = d²/2

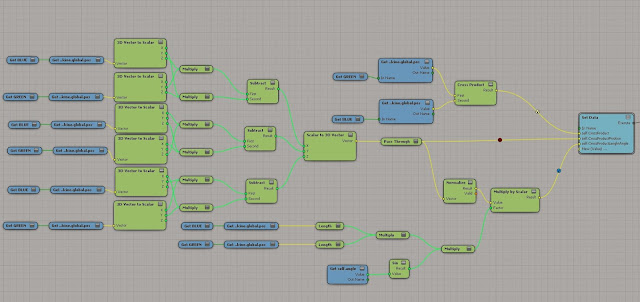
What this looks like in ICE ....

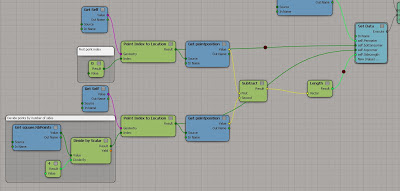
Side length

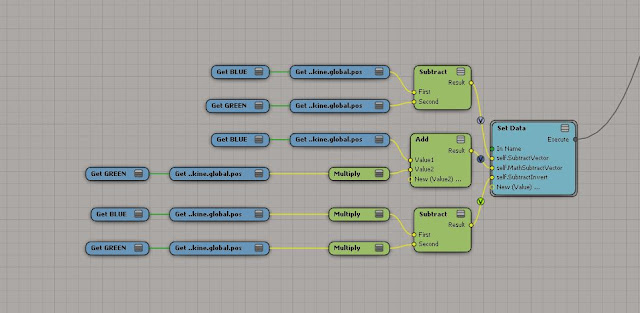
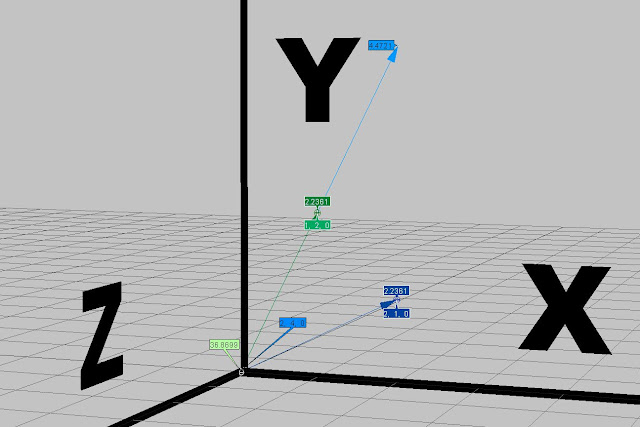
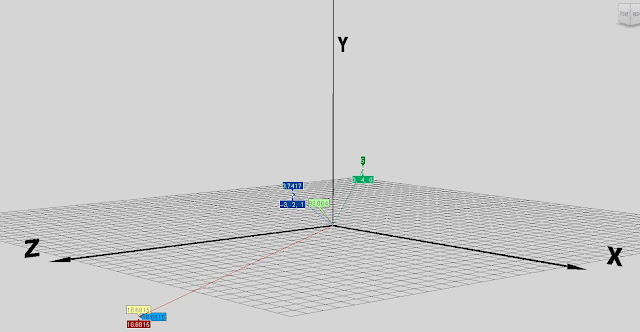
To work out the side length of the square shown below.....

..... Subtract the corner point (-1,-1,0) with corner point (-1,1,0). Then simply get the length of the vector between the them.

 

Perimeter

The light green perimeter value is worked out with the math sum shown below, while the darker green value shows the curve length attribute in ICE, they are both the same.

 

p = 4.a

Diagonal

The diagonal length as shown by the blue value below was got by....

d = a .  √2

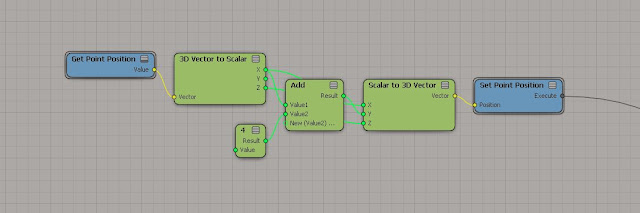
Area

 Area can be calculated two ways, by multiplying the side lengths or by the diagonal....

..... here are what those calculations look like in ICE.

The end :D

Circle Area

Circles....

Hula Hoop

The definition of a circle is:

The set of all points on a plane that are a fixed distance from a center.

*click too make bigger*

The Radius is the distance from the center to the edge.

The Diameter starts at one side of the circle, goes through the center and ends on the other side.

The Circumference is the distance around the edge of the circle.

The Chord is a line segment whose endpoints lie on the circle. 

The Tangent is a straight line that touches the circle at a single point.

When you divide the circumference by the diameter you get 3.141592654...
which is the irrational number π (Pi) 

thus :

Circumference = π × Diameter

Diameter =  π × Circumference

To get the area of a circle you need either the radius or the diameter and π .

The area of a circle is π times the radius squared, which is written:

A = π × r²

Or, in terms of the Diameter :

A = (π/4) × D²

A circle has about 80% of the area of a similar-width square.
The actual value is (π/4) = 0.785398... = 78.5398...%

Lets look at this in ICE 

I created a normal circle in Softimage with a radius of 1, and a subdivision count of 16.

*click too make bigger*

 The ICE attributes on a circle are quite limited, it pretty much only gives you the curve length. So if you want to know say... the area of the circle you will have to work it out for yourself. Here is how I got some of the values I wanted to know.

 π (Pi)

To get π I used the attribute curvelength (circumference) divided with the diameter (Got the distance between two opposite points on the circle).

*click too make bigger*

....you can see from the image below that got me the right value.

*click too make bigger*

 Radius

R = Diameter/2

*click too make bigger*

 

*click too make bigger*

 

 

Area 

The Blue value is area worked out with diameter and the Green value is area worked out with the radius.

 

*click too make bigger*

 They both get the same result.....

*click too make bigger*

Circumference 

The Purple value is worked out with the Math in the ICE tree below, where as the green value is the curve length given by the ICE attribute in Softimage.

*click too make bigger*

 They are both the same...

*click too make bigger*

Diameter

Calculating Diameter using the math sum :

D = r . 2

*click too make bigger*

*click too make bigger*

Unit Circle

 .....this is a really fun way tho see how a circle is a set of points that are a fixed distance from a center.

 

Functions In Ice

 

Functions

Functions represent relationships between variables. They take an input variable, manipulate it in some way and produce an output variable.

 

 

*click to make bigger*

 

The Input(X) can also be called: domain, domain elements, independent variable or argument.

The output(x+4) can also be called: range, image, range elements, dependent variables or value of function.

The relationship between (X) and x + 4 is F

Taking f(x) = x + 4 into ICE would look like the image below if f(x) = y.

*click to make bigger*

Before I applied the Function to a grid pointcloud it looked like the image below. All the points are at there initial position.  All the points read as 0,0,0 position, this is local position coordinates for every point, in the global coordinate space all the points except the middle point would have either 1 or -1 for its Z and X value. *The global value of right corner point would read as: -1 (X), 0 (Y), 1 (Z)*

*click to make bigger*

When I apply the function to the grid pointcloud it looks like the image below. Note how it added the global value of X not the local value. Then the + 4 giving us a graph that increases linearly in space. *You can see the global coordinate in the image below*

*click to make bigger*

 

 There are tons of cool functions to play around with on Thiano Costa's blog, I know I made all these functions and had tons of fun seeing how they react on different objects. 

Here are some more fun looking Functions

|cos(x+z)| ^ 10/2

 | cos(x^2+z^2) | ^ (1/2)

 cos( |x| + |z| ) * ( x + z )

 y = |cos(x) + cos(z)| ^ (1/2)

| cosx^2+cosz^2) | ^ (1/2)

 

Vector's and ICE

When I started this post I was only going to do an example of Dot Product in ICE, but it got a bit abstract and hard to follow. So ....

....in this post. So lets get cracking :D

 

A Vector

 

Vectors are use to represent physical quantities which have length(magnitude) and direction, like wind or gravity.

*click to make bigger*

A vector has direction and magnitude(length) 

Add Vectors 

 

 

A + B = B + A 

  When Adding Vectors imagine you are joining them head to tail, then getting the long side of the triangle they make. This new vector is also known as the resultant vector. *You can add as many vectors as you want together, it will always have a "straight arrow" resultant vector answer.*

*click to make bigger*

When adding vectors it doesn't matter which vector gets added first you will always get the same result.
In the Image below I show -the dark yellow arrow is the resultant vector, between the blue arrow vector and the green arrow vector- how this looks in ICE.

*click to make bigger*

To get the Inverse of A+B(resultant vector) all you need to do is : (-A) - B = Inverse of A + B
In other words get the negative value of blue vector, then subtract that from the green vector and you will get the inverse of A + B(resultant vector*purple arrow*).
Here's what the ICE nodes look like...

*click to make bigger*

Subtract Vectors

 

C  = B + (-A)

When we are subtracting vectors you have to invert the vector(green arrow vector) you want to subtract from the blue arrow vector, then add the two vectors together like normal.
The order you subtract in matters, meaning if you subtract them in the wrong order you will get a different answer to what you expect.  

*click to make bigger*

In ICE you can subtract vectors by just using the subtract node, or you can do it with the proper vector math I showed above, both get the same result as you can see with the two purple values in the image below.
To get the inverse of B + (-A) you have to do the following (-B) - (-A) = C
The light green arrow in the image below shows the inverse value of B + (-A)

*click to make bigger*

Here's what it looks like in the ICE tree...

*click to make bigger*

 

Multiply by Scalar

 

C  = 2(A)

 When you multiply a vector by a scalar its called "scaling", because you don't affect the direction but only the magnitude(length) of the vector. This makes the length "bigger" or "smaller", more "speed" or "less speed".

*click to make bigger*

In the images below and above, the light blue arrow and values represent the green arrow vector if scaled by the value 2.

*click to make bigger*

 

Cross Product

 

A · B = |a| × |b| × sin(θ) n

 *|a| means the magnitude (length) of vector A*
 *|b| means the magnitude (length) of vector B*

 

Cross product is a method of multiplying two vectors in 3d space, producing a vector that is perpendicular to both initial vectors. In physics it can be used to work out the torque of a force. You can also get the magnitude between two vectors this way :D 

*click to make bigger*

to visualise this we can use the right hand rule like in the image below

*click to make bigger*

 In ICE you get a ready made node to help you work out cross product(shown by the red vector arrow in the images below). I show what it would look like if we didn't have the ready made node with the light blue Value and the light Red value.

*click to make bigger*

As you can see from the image below the Yellow values is the normal cross product node. The Red value is from A · B. And the light Blue Value is from the |a| × |b| × sin(θ) n. Which all results in the same answer.
*On a side note if the angle between two vectors are 180 degrees the cross product will be zero*

*click to make bigger*

 

 

Scalar Product a.k.a Dot Product 

 

 A scalar product is an operation that combines two vectors(A.B) to create a scalar, a number with no direction.

*click to make bigger*

So by using a dot product we are multiplying(scaling) two vectors with each other, and end up with a scalar value (note not a vector value).

You can calculate the Dot Product of two vectors this way: 

A · B = |a| × |b| × cos(θ) 

 *|a| means the magnitude (length) of vector A*
 *|b| means the magnitude (length) of vector B*
 **You can only multiply vectors when they point in the same direction, to get A and B to point in the same direction we multiply by the cos(θ)** 
(multiply the length of |a| times the length of |b|, then multiply by the cosine of the angle between(θ) A and B)

Here's a fun Calculator I found that shows what the Vectors are doing when we multiply :D I played with it quite a bit.
Vector Calculator


  In the images below, although we are multiplying two vectors we end up with a scalar value of -1. This is because we as getting the dot product, not the cross product.

 

The Purple value shows the dot product nodes result in ICE, where as the light green value shows |a| × |b| × cos(θ) and the yellow value shows A · B. As you can see the answers are the same.
*On a side note when two vectors are at right angles to each other the dot product is zero.*

 

Ok, ok. So now your going like this is all really cool Math stuff, but how and what do I use this for in ICE, or just in general. :/ Cos the vector nodes in ICE pretty much does the math for you so why care right. Well, unless you know the math you won't ever really understand how powerful the vector nodes are. Once you get it you can fully utilise the nodes in ICE and use the math in other programs as well.

Unit Vector

A unit vector is a vector with a magnitude of one. It is also known as a normalized vector.

 

The pink Value shows how the normalize node makes the dark green vector value normalized, where the light green value shows how to normalize the dark green value using U = U / ||u||

Vectors get used for all kinds of things in ICE so get to know them as much as you can.

THE END