Circles....
 |
| Hula Hoop |
The definition of a circle is: |
|
|
|
The set of all points on a plane that are a fixed distance from a center.
 |
| *click too make bigger* |
|
|
|
|
The Radius is the distance from the center to the edge.
The Diameter starts at one side of the circle, goes through the center and ends on the other side.
The Circumference is the distance around the edge of the circle.
The Chord is a line segment whose endpoints lie on the circle.
The Tangent is a straight line that touches the circle at a single point.
When you divide the circumference by the diameter you get 3.141592654...
which is the irrational number π (Pi)
thus :
Circumference = π × Diameter
Diameter = π × Circumference
To get the area of a circle you need either the radius or the diameter and π .
The
area of a circle is
π times the radius squared, which is written:
A = π × r2
Or, in terms of the
Diameter :
A = (π/4) × D2
A circle has about 80% of the area of a similar-width square.
The actual value is (π/4) = 0.785398... = 78.5398...%
Lets look at this in ICE
I created a normal circle in Softimage with a radius of 1, and a subdivision count of 16.
 |
| *click too make bigger* |
The ICE attributes on a circle are quite limited, it pretty much only gives you the curve length. So if you want to know say... the area of the circle you will have to work it out for yourself. Here is how I got some of the values I wanted to know.
π (Pi)
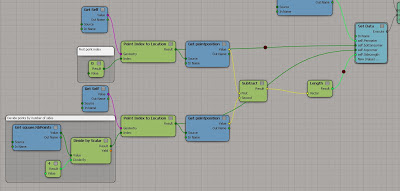
To get π I used the attribute curvelength (circumference) divided with the diameter (Got the distance between two opposite points on the circle).
 |
| *click too make bigger* |
....you can see from the image below that got me the right value.
 |
| *click too make bigger* |
Radius
R = Diameter/2
 |
| *click too make bigger* | |
 |
| *click too make bigger* | |
Area
The Blue value is area worked out with diameter and the Green value is area worked out with the radius.
 |
| *click too make bigger* |
They both get the same result.....
 |
| *click too make bigger* |
Circumference
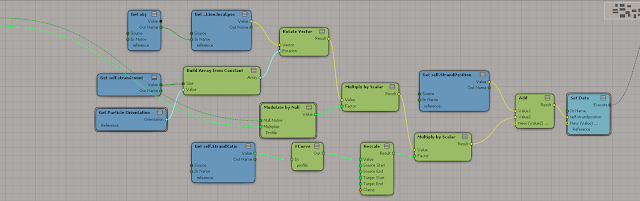
The Purple value is worked out with the Math in the ICE tree below, where as the green value is the curve length given by the ICE attribute in Softimage.
 |
| *click too make bigger* |
They are both the same...
 |
| *click too make bigger* |
Diameter
Calculating Diameter using the math sum :
D = r . 2
 |
| *click too make bigger* |
 |
| *click too make bigger* |
.....this is a really fun way tho see how a circle is a set of points that are a fixed distance from a center.