Vector's and ICE

When I started this post I was only going to do an example of Dot Product in ICE, but it got a bit abstract and hard to follow. So ....

....in this post. So lets get cracking :D

 

A Vector

 

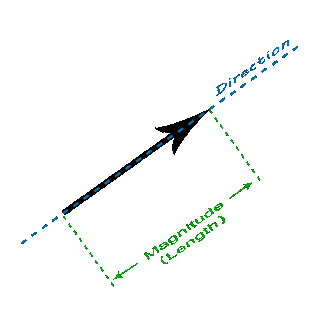
Vectors are use to represent physical quantities which have length(magnitude) and direction, like wind or gravity.

*click to make bigger*

A vector has direction and magnitude(length) 

Add Vectors 

 

 

A + B = B + A 

  When Adding Vectors imagine you are joining them head to tail, then getting the long side of the triangle they make. This new vector is also known as the resultant vector. *You can add as many vectors as you want together, it will always have a "straight arrow" resultant vector answer.*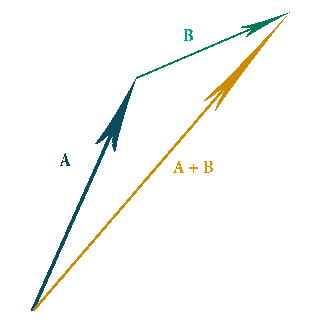

*click to make bigger*

When adding vectors it doesn't matter which vector gets added first you will always get the same result.
In the Image below I show -the dark yellow arrow is the resultant vector, between the blue arrow vector and the green arrow vector- how this looks in ICE.

*click to make bigger*

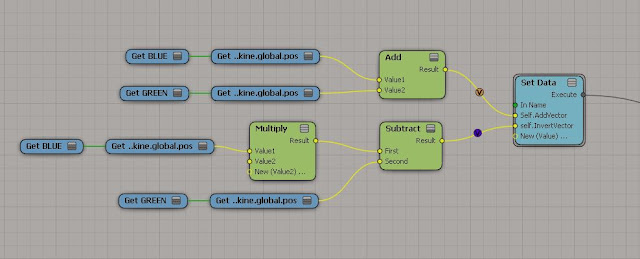
To get the Inverse of A+B(resultant vector) all you need to do is : (-A) - B = Inverse of A + B
In other words get the negative value of blue vector, then subtract that from the green vector and you will get the inverse of A + B(resultant vector*purple arrow*).
Here's what the ICE nodes look like...

*click to make bigger*

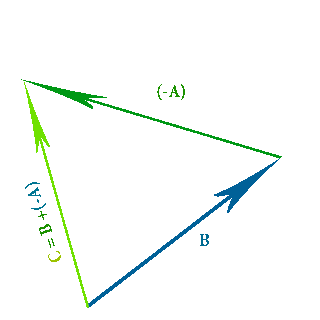
Subtract Vectors

 

C  = B + (-A)

When we are subtracting vectors you have to invert the vector(green arrow vector) you want to subtract from the blue arrow vector, then add the two vectors together like normal.
The order you subtract in matters, meaning if you subtract them in the wrong order you will get a different answer to what you expect.  

*click to make bigger*

In ICE you can subtract vectors by just using the subtract node, or you can do it with the proper vector math I showed above, both get the same result as you can see with the two purple values in the image below.
To get the inverse of B + (-A) you have to do the following (-B) - (-A) = C
The light green arrow in the image below shows the inverse value of B + (-A)

*click to make bigger*

Here's what it looks like in the ICE tree...

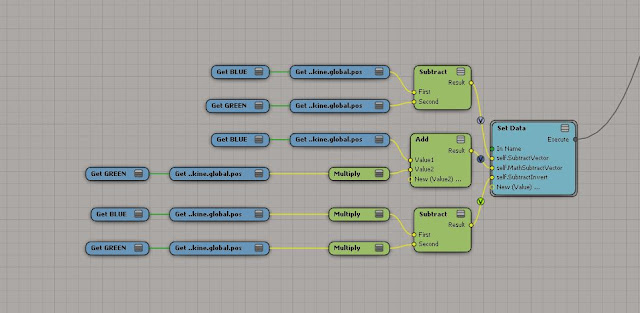*click to make bigger*

 

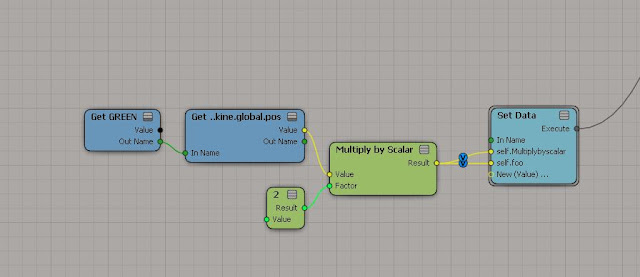
Multiply by Scalar

 

C  = 2(A)

 When you multiply a vector by a scalar its called "scaling", because you don't affect the direction but only the magnitude(length) of the vector. This makes the length "bigger" or "smaller", more "speed" or "less speed".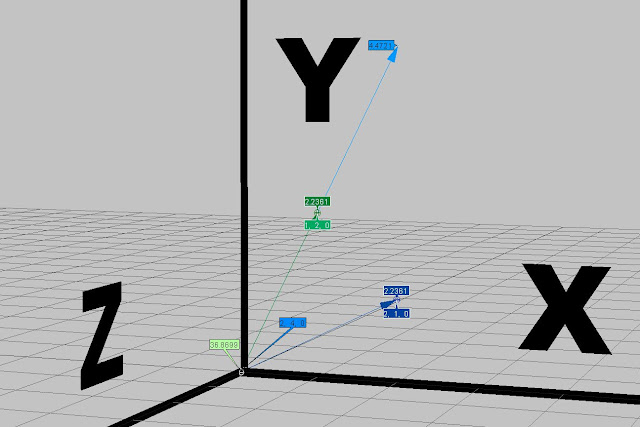

*click to make bigger*

In the images below and above, the light blue arrow and values represent the green arrow vector if scaled by the value 2.

*click to make bigger*

 

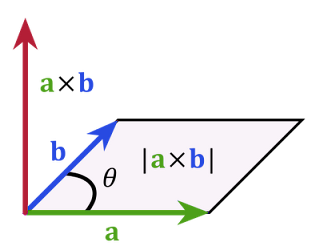
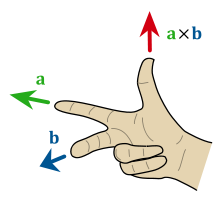
Cross Product

 

A · B = |a| × |b| × sin(θ) n

 *|a| means the magnitude (length) of vector A*
 *|b| means the magnitude (length) of vector B*

 

Cross product is a method of multiplying two vectors in 3d space, producing a vector that is perpendicular to both initial vectors. In physics it can be used to work out the torque of a force. You can also get the magnitude between two vectors this way :D 

*click to make bigger*

to visualise this we can use the right hand rule like in the image below

*click to make bigger*

 In ICE you get a ready made node to help you work out cross product(shown by the red vector arrow in the images below). I show what it would look like if we didn't have the ready made node with the light blue Value and the light Red value.

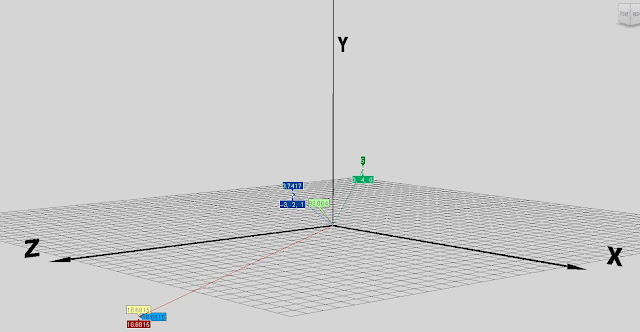*click to make bigger*

As you can see from the image below the Yellow values is the normal cross product node. The Red value is from A · B. And the light Blue Value is from the |a| × |b| × sin(θ) n. Which all results in the same answer.
*On a side note if the angle between two vectors are 180 degrees the cross product will be zero*

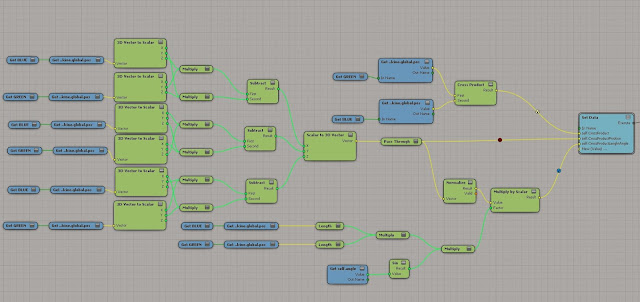*click to make bigger*

 

 

Scalar Product a.k.a Dot Product 

 

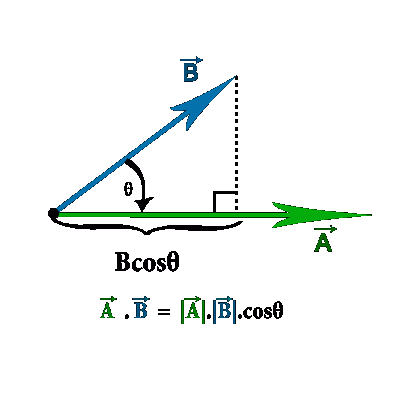
 A scalar product is an operation that combines two vectors(A.B) to create a scalar, a number with no direction.

*click to make bigger*

So by using a dot product we are multiplying(scaling) two vectors with each other, and end up with a scalar value (note not a vector value).

You can calculate the Dot Product of two vectors this way: 

A · B = |a| × |b| × cos(θ) 

 *|a| means the magnitude (length) of vector A*
 *|b| means the magnitude (length) of vector B*
 **You can only multiply vectors when they point in the same direction, to get A and B to point in the same direction we multiply by the cos(θ)** 
(multiply the length of |a| times the length of |b|, then multiply by the cosine of the angle between(θ) A and B)

Here's a fun Calculator I found that shows what the Vectors are doing when we multiply :D I played with it quite a bit.
Vector Calculator


  In the images below, although we are multiplying two vectors we end up with a scalar value of -1. This is because we as getting the dot product, not the cross product.

 

The Purple value shows the dot product nodes result in ICE, where as the light green value shows |a| × |b| × cos(θ) and the yellow value shows A · B. As you can see the answers are the same.
*On a side note when two vectors are at right angles to each other the dot product is zero.*

 

Ok, ok. So now your going like this is all really cool Math stuff, but how and what do I use this for in ICE, or just in general. :/ Cos the vector nodes in ICE pretty much does the math for you so why care right. Well, unless you know the math you won't ever really understand how powerful the vector nodes are. Once you get it you can fully utilise the nodes in ICE and use the math in other programs as well.

Unit Vector

A unit vector is a vector with a magnitude of one. It is also known as a normalized vector.

 

The pink Value shows how the normalize node makes the dark green vector value normalized, where the light green value shows how to normalize the dark green value using U = U / ||u||

Vectors get used for all kinds of things in ICE so get to know them as much as you can.

THE END