Beautiful broken fur

*click to make bigger*

Forgot to set int Groom O_O sooooo pretty

Cool post from Chris Cunnington :D

Chris Cunnington

http://blog.cunnington.co.za/2012/09/27/stereoscopic-depth-compression/


Chris is the Stereo Guru at Triggerfish. His also very good at growing Orchid *Which is quite hard to do O_O*

Change is good...

Change?!

While waiting for renders and caches I looked at my blog and thought to myself, it needs to be simplified a bit :D And now it is.... hopefully it looks better. Atlest I think it does

Vector's and ICE

When I started this post I was only going to do an example of Dot Product in ICE, but it got a bit abstract and hard to follow. So ....

....in this post. So lets get cracking :D

 

A Vector

 

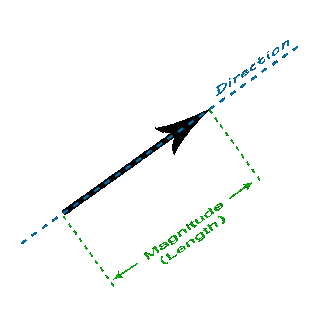
Vectors are use to represent physical quantities which have length(magnitude) and direction, like wind or gravity.

*click to make bigger*

A vector has direction and magnitude(length) 

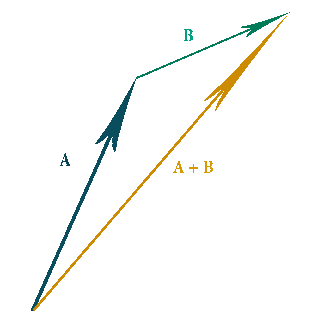
Add Vectors 

 

 

A + B = B + A 

  When Adding Vectors imagine you are joining them head to tail, then getting the long side of the triangle they make. This new vector is also known as the resultant vector. *You can add as many vectors as you want together, it will always have a "straight arrow" resultant vector answer.*

*click to make bigger*

When adding vectors it doesn't matter which vector gets added first you will always get the same result.
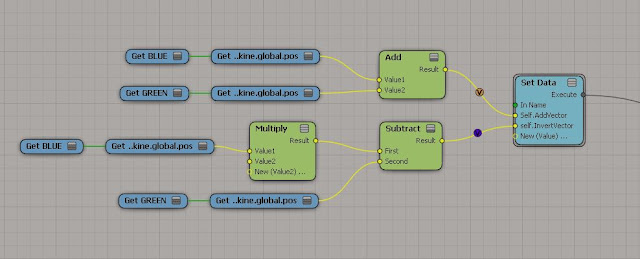
In the Image below I show -the dark yellow arrow is the resultant vector, between the blue arrow vector and the green arrow vector- how this looks in ICE.

*click to make bigger*

To get the Inverse of A+B(resultant vector) all you need to do is : (-A) - B = Inverse of A + B
In other words get the negative value of blue vector, then subtract that from the green vector and you will get the inverse of A + B(resultant vector*purple arrow*).
Here's what the ICE nodes look like...

*click to make bigger*

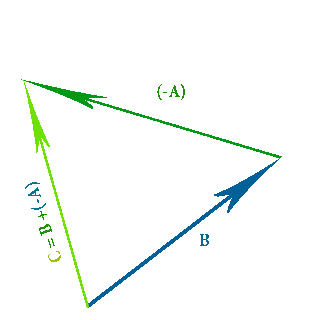
Subtract Vectors

 

C  = B + (-A)

When we are subtracting vectors you have to invert the vector(green arrow vector) you want to subtract from the blue arrow vector, then add the two vectors together like normal.
The order you subtract in matters, meaning if you subtract them in the wrong order you will get a different answer to what you expect.  

*click to make bigger*

In ICE you can subtract vectors by just using the subtract node, or you can do it with the proper vector math I showed above, both get the same result as you can see with the two purple values in the image below.
To get the inverse of B + (-A) you have to do the following (-B) - (-A) = C
The light green arrow in the image below shows the inverse value of B + (-A)

*click to make bigger*

Here's what it looks like in the ICE tree...

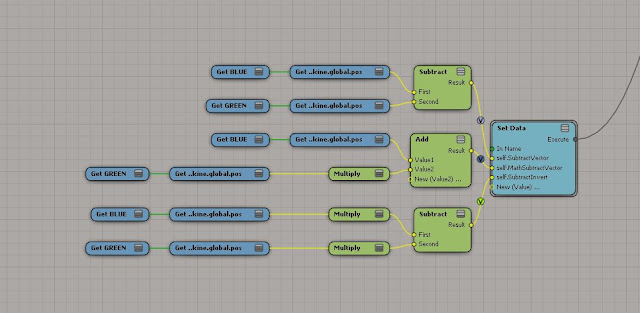*click to make bigger*

 

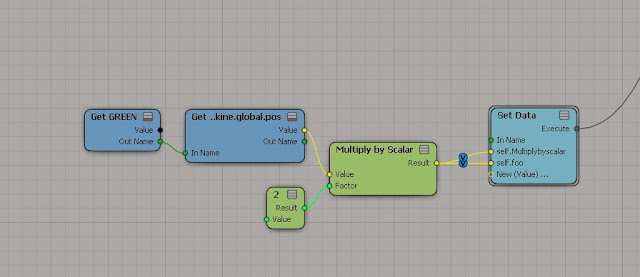
Multiply by Scalar

 

C  = 2(A)

 When you multiply a vector by a scalar its called "scaling", because you don't affect the direction but only the magnitude(length) of the vector. This makes the length "bigger" or "smaller", more "speed" or "less speed".

*click to make bigger*

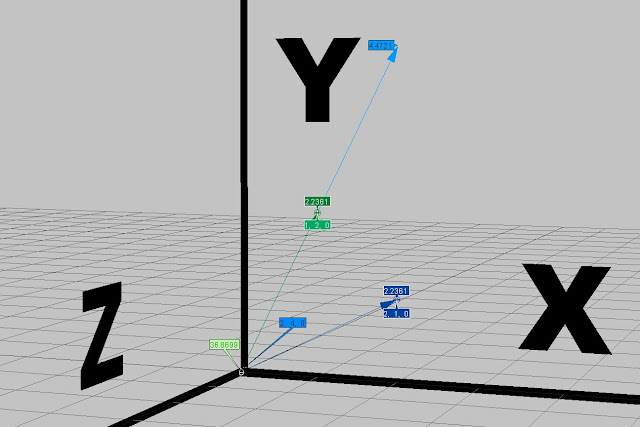
In the images below and above, the light blue arrow and values represent the green arrow vector if scaled by the value 2.

*click to make bigger*

 

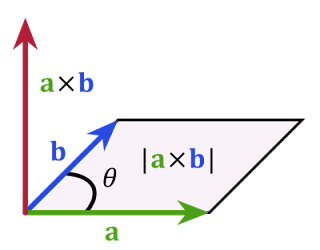
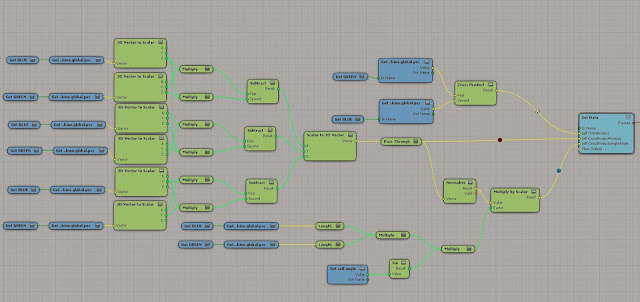
Cross Product

 

A · B = |a| × |b| × sin(θ) n

 *|a| means the magnitude (length) of vector A*
 *|b| means the magnitude (length) of vector B*

 

Cross product is a method of multiplying two vectors in 3d space, producing a vector that is perpendicular to both initial vectors. In physics it can be used to work out the torque of a force. You can also get the magnitude between two vectors this way :D 

*click to make bigger*

to visualise this we can use the right hand rule like in the image below

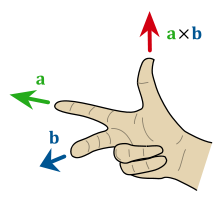*click to make bigger*

 In ICE you get a ready made node to help you work out cross product(shown by the red vector arrow in the images below). I show what it would look like if we didn't have the ready made node with the light blue Value and the light Red value.

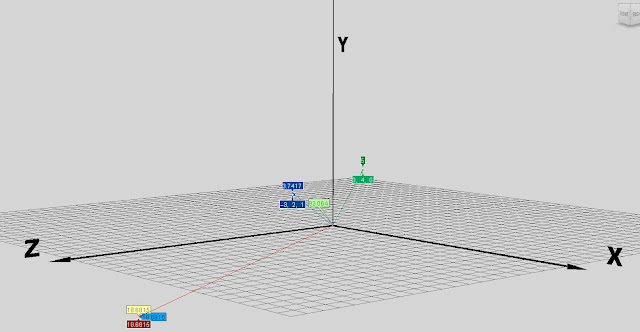*click to make bigger*

As you can see from the image below the Yellow values is the normal cross product node. The Red value is from A · B. And the light Blue Value is from the |a| × |b| × sin(θ) n. Which all results in the same answer.
*On a side note if the angle between two vectors are 180 degrees the cross product will be zero*

*click to make bigger*

 

 

Scalar Product a.k.a Dot Product 

 

 A scalar product is an operation that combines two vectors(A.B) to create a scalar, a number with no direction.

*click to make bigger*

So by using a dot product we are multiplying(scaling) two vectors with each other, and end up with a scalar value (note not a vector value).

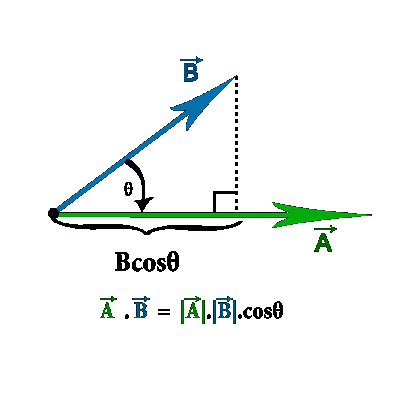
You can calculate the Dot Product of two vectors this way: 

A · B = |a| × |b| × cos(θ) 

 *|a| means the magnitude (length) of vector A*
 *|b| means the magnitude (length) of vector B*
 **You can only multiply vectors when they point in the same direction, to get A and B to point in the same direction we multiply by the cos(θ)** 
(multiply the length of |a| times the length of |b|, then multiply by the cosine of the angle between(θ) A and B)

Here's a fun Calculator I found that shows what the Vectors are doing when we multiply :D I played with it quite a bit.
Vector Calculator


  In the images below, although we are multiplying two vectors we end up with a scalar value of -1. This is because we as getting the dot product, not the cross product.

 

The Purple value shows the dot product nodes result in ICE, where as the light green value shows |a| × |b| × cos(θ) and the yellow value shows A · B. As you can see the answers are the same.
*On a side note when two vectors are at right angles to each other the dot product is zero.*

 

Ok, ok. So now your going like this is all really cool Math stuff, but how and what do I use this for in ICE, or just in general. :/ Cos the vector nodes in ICE pretty much does the math for you so why care right. Well, unless you know the math you won't ever really understand how powerful the vector nodes are. Once you get it you can fully utilise the nodes in ICE and use the math in other programs as well.

Unit Vector

A unit vector is a vector with a magnitude of one. It is also known as a normalized vector.

 

The pink Value shows how the normalize node makes the dark green vector value normalized, where the light green value shows how to normalize the dark green value using U = U / ||u||

Vectors get used for all kinds of things in ICE so get to know them as much as you can.

THE END

Backface Culling/Clipping of ICE Strands

 

Backface Culling

In computer graphics backface culling determines whether something is "visible" in the camera's field of view. This process makes rendering fur a lot quicker as you only render the fur that is "seen" instead of rendering the fur that is hidden from the camera.

Image U is what the Camera sees.....

Image U

 

*click on image to make it bigger*

  If there was no backface culling there would be a lot of fur in the scene to calculate. Like in the Image F....

  Image F

 

*click on image to make it bigger* 

But if you use ICE to create backface culling you can reduce the amount of fur that the renderer needs to calculate by quite a lot, as you can see from Image Y...

Image Y

 

*click on image to make it bigger* 

So how do we do Backface Culling and Clipping in ICE?

The most common way of calculating "backface culling", would be to use a "dot product" to determine the normals of the mesh the fur is grown from then delete the fur that is not "seen" by the camera.
As you can see from the image below named "Clipping" we can see that Clipping deletes the fur that is outside the F.O.V of the camera, shown by the blue lines.  For the actual "Culling" I used a similar approach to the dot product, but ignore the edge of the cameras F.O.V. Instead we focus on the side of the object that faces away from the camera, illustrated by the red line in the image called "Culling".


"Clipping"

 

*click on image to make it bigger*  

"Culling"

 

*click on image to make it bigger*   

When you combine the two you get Image Y, shown earlier.

Lets take a look at ICE and see how this all gets done.  Here in Image Q is the node we used on Khumba to Cull the fur.

Image Q

 

*click on image to make it bigger* 

The Red Square is a scalar that makes it possible for us to adjust the Culling after we added the original values from the camera, just like a fall off.
The Blue Square is exactly the same except it gives us a fall off for the Clipping.

So within ICE we can adjust the Field Of View(F.O.V) as we need it. Without having to touch the camera settings/setup's. The Blue lines in Images H,J and I represent the actual camera F.O.V, while the Red lines shows how ICE adjusts the F.O.V.

Image H

  

*click on image to make it bigger*  

Image J

 

*click on image to make it bigger*  

 Image I

 

*click on image to make it bigger*  

 

When we explore inside, the node is made up of three sections, Image A and Image B and then brought together with Image C

Image A

 

*click on image to make it bigger*  

Image A has to do with the Culling. We get the angle between the emitter object and the camera (inside the Blue square), then we get the angle of the Field of View of the camera (inside the Red square),  using the greater than or equal to Boolean node (inside the Orange square) we say that anything outside that angle gets deleted. So imagine a Triangle, everything inside the triangle stays, everything outside goes (deleted).

Image B deals with the clipping of the fur. Here we use a standard node in ICE called "Test Visibility From Camera", we have modified it a bit to work for our needs. We obviously don't just want to test visibility from the camera when it comes to culling fur. It works out the length of the four sides of the camera view (inside the Red square) -- making a square in space -- using a dot product sum between the fur (inside the Blue square) and the camera (inside the Green square), then we just say delete everything outside of that square (inside the Yellow square). To do this we need the cameras position in space (inside the Green square) and the F.O.V and aspect ratio of the camera (inside the Purple square).


Image B

 *click on image to make it bigger* 

Image C brings the Culling and the Clipping together with an IF statement. If there is fur inside the clipping square that is behind the character then that fur will also get deleted.


 Image C

 *click on image to make it bigger*

This is what it all looks like over time with a moving camera.

And that is culling fur in a nut shell. There are tons of Clipping Algorithms
that you can go look at here

:D

Story Elements ...... He he he

*click on image to make bigger*

I like this :D

Random commecial.....

the Khumba fur nodes where used by Luma for a really funny add by Cadbury...

Its nice seeing other people using our ICE nodes to make cool stuff

:D

The company in Cape Town I work at...

TriggerFish Animation Studio

www.triggerfishstudios.com 

TA DA!!!! \:D/

Boolean...

Boolean is a data type in ICE, having two values(normally being true or false) 0 or 1. They are intended to be used as truth values *hit or miss* and so on.

Here's what they look like in ICE...

*click to make bigger*

The top Boolean is a true, false node. The ports are Orange, I often use this node in connection with a  if  statement. For example, if the Camera sees the fur, it will display, if not it should be deleted.

You also get : Exclusive Or,Or,Not, And nodes, which look like .....  

*click to make bigger*

To understand the And, Or, Not nodes is easy enough...

*click to make bigger*

But when you working in ICE with a million strands, it is easy to forget even how Boolean works. >_<

Randomness for the day ^-^